В статье обсуждается практическая программная реализация предложенного автором нового универсального метода расчета стержневых систем, основанного на машинном аналитическом интегрировании большого количества связанных дифференциальных уравнений в дискретных системах – стержневых конструкциях. Метод реализован в экспериментальном авторском программном обеспечении.
Приведен сравнительный анализ некоторых ключевых решений для произвольной тестовой конструкции с симметрией в геометрии и характере нагружения. Адекватность результатов проверена в промышленном пакете конечноэлементного анализа AutodeskRobotStructural Analysis[1].
This article deals with the practical programming realization of a new universal method of designing bar systems. The method is based on computer-aided analytical integration of plenty of interconnected differential equations in discrete systems-bar structures. The method is embodied in the author’s experimental software.
The comparative analysis of some key solutions for an unspecified test structure with symmetry in geometry and loading pattern has been carried out. The adequacy of the results has been verified by using a commercial software package of finite element analysis i. e. Autodesk Robot Structural Analysis.
ВВЕДЕНИЕ
Метод расчета в механике стержневых систем [1] основан на машинном аналитическом интегрировании большого количества связанных дифференциальных уравнений в дискретных системах – стержневых конструкциях. Существует множество частных приемов и методик расчета как отдельных стержней, так и сложных стержневых систем. Широкий их обзор приведен в [2]. Однако существует лишь три основополагающих подхода к расчету таких систем.
1. Метод интегрирования дифференциального уравнения. Идея заключается в составлении дифференциального уравнения, получении его общего решения и затем использовании граничных условий для вычисления постоянных интегрирования. Впервые дифференциальное уравнение линии прогибов было применено при расчете балок в работе Навье [3], о чем упоминает в своей механике материалов С. П. Тимошенко.
2. Приемы, основанные на применении первой теоремы Кастилиано. Фундаментальным расширением первой теоремы Кастилиано является принцип стационарности потенциальной энергии, применение которого приводит к уравнениям равновесия так называемого метода перемещений. В случае линейно деформируемых конструкций метод иногда называют методом жесткостей.
3. Методы, основанные на теореме Кротти – Энгессера и второй теореме Кастилиано. Они приводят к уравнениям принципа стационарности дополнительной энергии. Для нелинейно деформируемых конструкций принцип стационарности записывается через дополнительную энергию, а для линейно упругих конструкций – через энергию деформации. Соответственно в первом случае принцип стационарности составляет основу метода сил, а во втором – основу того же метода, который принято называть методом податливостей. В отличие от метода перемещений, уравнения которого представляют собой уравнения равновесия в силах, уравнения метода сил имеют смысл уравнений совместности перемещений.
ОБЗОР ТЕОРЕТИЧЕСКИХ ОСНОВ И АКТУАЛЬНОСТЬ ИССЛЕДОВАНИЙ
Универсальным методом расчета в механике деформируемого тела является метод конечных элементов (МКЭ), основанный, в общем случае, на угадывании деформированной формы и, в частном случае, – для анализа стержневых систем (представляет собой машинную реализацию метода перемещений).
Пожалуй, не имеет смысла обсуждать преимущества и недостатки МКЭ. Объективно надо признать, что прогресс в решении множества задач механики деформируемого твердого тела достигнут именно благодаря этому методу. Тем не менее следует отметить очевидный недостаток МКЭ – его «стационарность». Исходные данные задачи и полученные решения – массивы чисел. Это обстоятельство значительно усложняет решение задач проектирования и оптимизации, особенно на этапе выбора и утверждения формы конструкции.
Стержневые системы обладают весьма высокой удельной по отношению к весу прочностью, технологичны при транспортировании и монтаже. К недостаткам принято относить относительную дороговизну производства элементов конструкции. В последнее время довольно часто в городах Беларуси можно наблюдать процесс сборки стержневых систем, подобный приведенному на рис. 1.
Рис. 1. Пример каркасной стержневой конструкции
Заявляемый подход относится к аналитическим, не численным методам исследования в традиционной классификации. Основное преимущество аналитических методов исследования состоит в том, что они дают ясное представление о взаимосвязи параметров конструкции с ее несущей способностью, возможность параметрического анализа и формулировки новых закономерностей. Распространенность стержневых конструкций в качестве несущих каркасов и преимущества аналитического описания поведения сложных объектов определяют актуальность исследований.
ПОСТАНОВКА ПРОБЛЕМЫ
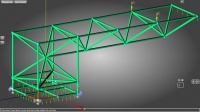
Рассмотрим симметричную стержневую конструкцию произвольного вида, нагруженную сосредоточенными силами F = 15 000 Н и распределенными нагрузками q = 10 000 Н/м так, как показано на рис. 2.
Не нарушая общности анализа, примем, что все элементы конструкции – невесомые стержни круглого поперечного сечения. Материал стержней – линейно упругий, модель предполагает работу конструкции в области выполнения закона Гука при заданных нагрузках. Характеристики геометрии и материала стержней представлены в таблице 1.
Таблица 1. Характеристики стержней конструкции
| Характеристика | Значение |
|---|---|
| Модуль Юнга E, Па | 2,05×1011 |
| Коэффициент Пуассона n | 0,3 |
| Модуль сдвига G, Па | G = E/(2×[1 + n]) = 0,7885×1011 |
| Диаметр d, см | 4,0 |
| Осевой момент инерции Ix, см4 | Ix = pd 4/64 = 12,566×10-8 |
| Осевой момент инерции Iy, см4 | Iy = pd 4/64 = 12,566×10-8 |
| Осевой момент инерции Iz, см4, z – ось стержня | Iz = pd 4/32 = 25,133×10-8 |
| Площадь поперечного сечения A, см2 | А = pd 2/4 = 12,566×10-4 |
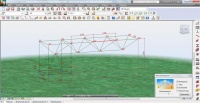
Основные габаритные размеры исследуемой стержневой системы показаны в окне программы Autodesk Robot StructuralAnalysis (рис. 3).
Поставим задачу определить в двух программных средах реакции в четырех опорах, а также провести сравнительный анализ внутренних силовых факторов в отмеченном на рис. 2 стержне 1 и анализ перемещений в стержне 2.
Выделенные стержни 1 и 2 предназначены для уточненного верификационного анализа
Рис. 2. Общий вид тестовой конструкции. Экспериментальное программное обеспечение
Рис. 3. Общий вид тестовой конструкции. Программное обеспечение Autodesk Robot Structural Analysis
РЕШЕНИЕ И АНАЛИЗ РЕЗУЛЬТАТОВ
Заметим, что симметрия в геометрии конструкции и характере нагружения должна приводить к одинаковым значениям как реакций, так и величин внутренних факторов, в том числе перемещений. Так, например, абсолютные величины реакций в опорах 1 и 9, а также в опорах 3 и 6 не должны отличаться между собой (см. рис. 3).
Полученные в двух программах (Robot и экспериментальное программное обеспечение (ЭПО)) значения реакций сведем в таблицу 2. Следует зметить, что в каждой из программных сред системы координат отличаются, поэтому, принимая во внимание указанную особенность, будем обращать внимание лишь на абсолютные значения.
Таблица 2. Сравнительный анализ реакций в опорах конструкции
| Реакция в опоре, Н | |||||
|---|---|---|---|---|---|
| Узел (Robot/ЭПО) | Реакция | ЭПО | Robot | Относительная ошибка ЭПО – Robot, % | |
| I группа симметричных опор | |||||
| 1/2 | Rx | 23393,50 | 23395,16 | 0,0071 | |
| Ry | 23391,00 | 23392,70 | 0,0073 | ||
| Rz | 149140,00 | 149142,14 | 0,0014 | ||
| 9/9 | Rx | 23393,50 | 23395,16 | 0,0071 | |
| Ry | -23391,00 | -23392,70 | 0,0073 | ||
| Rz | 149140,00 | 149142,14 | 0,0014 | ||
| II группа симметричных опор | |||||
| 3/3 | Rx | -23393,50 | -23395,16 | 0,0071 | |
| Ry | 23361,40 | 23363,06 | 0,0071 | ||
| Rz | 4140,01 | 4142,14 | 0,0514 | ||
| 6/7 | Rx | -23393,50 | -23395,16 | 0,0071 | |
| Ry | -23361,40 | -23363,06 | 0,0071 | ||
| Rz | 4140,01 | 4142,14 | 0,0514 | ||
Данные таблицы 2 свидетельствуют о том, что экспериментальное программное обеспечение, в основе которого лежат теоретические обоснования, изложенные в [1, 4], позволяет получить абсолютно корректные результаты. Более того, ЭПО генерирует одинаковые значения реакций в симметричных опорах – первой и девятой, а также в третьей и шестой (см. рис. 3). Следует отметить, что внутренняя (численная) ошибка в определении реакций проявляется лишь в седьмом знаке после запятой (ЭПО). В целом отмечается полное совпадение результатов, найденных с помощью двух программных сред: экспериментальной системы и продукта компании Autodesk.
Обратимся к внутренним факторам в стержне 1 (см. рис. 2). Заметим, что локальные системы координат для стержней в программах отличаются, различны также правила знаков для изгибающих моментов в том смысле, что в системе AutodeskRobot Structural Analysis эпюры изгибающих моментов строятся по умолчанию на растянутом волокне, в экспериментальном программном обеспечении – на сжатом. Внутренние факторы в граничных точках стержня 1 (см. рис. 2) представлены в таблице 3. При этом сохранены знаки факторов каждой из систем анализа. Однако сравнение проводится для величин одной природы и истинного направления. Как следует из данных таблицы 3, результаты в полной мере совпадают, ошибка всюду не превышает сотой доли одного процента.
Таблица 3. Сравнение значений внутренних силовых факторов
| Внутренний фактор (по локальной системе координат Robot) | ЭПО | Robot | Относительная ошибка, % |
|---|---|---|---|
| Продольная сила N, Н | 25850,61 | -25848,48 | 0,0082 |
| Поперечная сила Qy, Н | 23358,72 | -23360,41 | 0,0072 |
| Поперечная сила Qz, Н | -23393,98 | 23395,67 | 0,0072 |
| Изгибающий момент My, Н×м | 6108,10–(-5588,89) | (-6108,17)–5589,66 | 0,0011–0,0138 |
| Изгибающий момент Mz, Н×м | 6115,45–(-5563,91) | (-6115,52)–5564,69 | 0,0011–0,0140 |
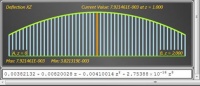
Следует отметить, что основное преимущество перед существующими системами МКЭ анализа состоит в возможности получения решений самого общего – аналитического или функционального вида. На рис. 4 представлен снимок с экрана, характеризующий распределение внутренних факторов в стержне 1 (см. рис. 2) – результат сгенерирован в экспериментальной программе.
Рис. 4. Эпюры внутренних силовых факторов для выделенного стержня 1 (см. рис. 2). Экспериментальное программное обеспечение
Перейдем к анализу перемещений в стержне 2 (см. рис. 2). В качестве ключевых точек тестирования примем граничные и срединное сечения балки. Результаты расчетов сведены в таблицу 4.
Таблица 4. Сравнение перемещений для выделенного стержня 2 (см. рис. 2) в глобальной системе координат
| Система координат Robot | Перемещение, см | ||
|---|---|---|---|
| Ux (горизонтальное) | Uy (вдоль стержня) | Uz (вертикальное) | |
| Robot (удаленная точка) | -0,3821 | -0,0033 | -3,9163 |
| ЭПО | 0,3821 | 0,0033 | -3,9163 |
| Ошибка, % | 0,0000 | 0,0000 | 0,0000 |
| Robot (ближняя точка) | -0,3821 | 0,0033 | -3,9163 |
| ЭПО | 0,3821 | -0,0033 | -3,9163 |
| Ошибка, % | 0,0000 | 0,0000 | 0,0000 |
| Robot (срединное сечение) | -0,7921 | 0,0000 | -7,8737 |
| ЭПО | 0,7921 | 0,0000 | -7,8736 |
| Ошибка, % | 0,0000 | 0,0000 | 0,0013 |
Как следует из таблицы 4, результаты, полученные в ЭПО и системе промышленного анализа Autodesk Robot StructuralAnalysis, находятся в полном соответствии друг с другом.
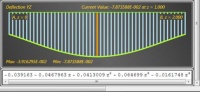
На рис. 5 представлены зависимости прогибов в двух плоскостях изгиба от текущей координаты z стержня, а также функция продольного перемещения (удлинения).
Рис. 5. Функции перемещений. Экспериментальное программное обеспечение
Функции перемещений, показанные на рис. 5, принципиально не содержат ошибок, за исключением машинно-предопределенных округлений. Если входными параметрами задачи являются символы (полностью или частично), то результатом расчета будут соответствующие формулы – зависимости, состоящие из символов (полностью или частично). Пример полностью символьного анализа стержневой конструкции приведен в работе [4].
ЗАКЛЮЧЕНИЕ
Достоинства предлагаемого подхода, основанного на символьном интегрировании дифференциального уравнения деформирования, очевидны. Аналитическое решение всегда предпочтительнее любого численного результата, особенно при выявлении закономерностей поведения и в оптимизационных мультивариантных задачах. Конечно, общий вид решения для большого числа сопряженных граничных условий может оказаться громоздким и сложным для восприятия. Анализ исследуемых зависимостей естественно проводить аналитически машинным способом. Точечную проверку найденных решений можно осуществить сравнением с тестовыми результатами, полученными в МКЭ средах, а также обратной подстановкой и соблюдением качественных закономерностей.
К условным недостаткам можно отнести машинные затраты на получение решений самого общего вида.
СПИСОК ЛИТЕРАТУРЫ
1. Орлов, С. А. Новый метод расчета в механике стержневых систем / С. А. Орлов // Вестник БелГУТа, г. Гомель. – 2004. – № 2(9). – С. 29–34.
2. Громыко, О. В. Расчет регулярных ферменных конструкций по континуальной схеме / О. В. Громыко. – Минск: БГУ, 2004. − 192 с.
3. Navier, L. M. H. Rеsumе des lecons donnеes а l¢еcole des ponts et chausses sur l¢application de la mеcanique а l¢еtablissement des constructions et des machines. Paris, Chez Carilian-Goeury, 3me ed. avec des notes et appendices par M. Barrе Saint-Venant: Paris, Dunod, 1864.
4. Орлов, С. А. Символьно-аналитический подход к анализу задач строительной механики / С. А. Орлов // Строительная наука и техника. − 2010. − № 4. − С. 47–50.