В статье излагаются критерии соответствия конечных элементов континуальных объектов и эквивалентных шарнирно-стержневых структур. Предлагаются усовершенствованные численно-аналитические методы расчета напряженно-деформированного состояния и оптимизации строительных сооружений. Рассматриваются специальные вопросы колебаний и устойчивости линейно и нелинейно (физически, геометрически, конструктивно, топологически и т. д.) деформируемых плоских и пространственных шарнирно-стержневых систем.

This article sets out compliance criteria for the finite elements of the continual objects and the equivalent hinged-rod structures. Advanced numerical-analytical methods have been offered for calculating the stress-strain state and optimization of the constructions. Special problems of vibrations and stability of linear and non-linear (physically, geometrically, structurally, topologically, etc.) deformable flat and spatial hinged-rod systems have been considered.

ВВЕДЕНИЕ

Замкнутое аналитическое решение для задачи определения напряженно-деформированного состояния сложной строительной конструкции получить, как правило, невозможно. По этой причине на современном этапе развития строительной механики и компьютерных технологий наиболее востребованными оказались численные методы и, в частности, метод конечных элементов. Обширная библиотека разнообразных линейных и нелинейных конечных элементов, реализованная в большом числе проектно-вычислительных комплексов, позволяет решать достаточно сложные задачи.

В то же время для нелинейных расчетов на прочность и жесткость, устойчивость и колебания, а также для решения задач оптимизации строительных сооружений, как показала практика [1–4], исключительно полезными оказались физические и математические модели, основанные на преобразовании расчетных схем континуальных объектов к шарнирно-стержневым схемам-аналогам, теория расчета которых в линейной и нелинейной постановках в настоящее время разработана наиболее полно [3]. Эквивалентные соотношения между конечными элементами континуальных объектов и соответствующими шарнирно-стержневыми блоками могут быть установлены по различным критериям, основным из которых следует считать энергетический. Кроме того, в инженерной практике и научных исследованиях применяют критерии равенства перемещений характерных узловых точек, равенства обобщенных усилий, а также смешанные.

При создании математических моделей физически нелинейных деформируемых объектов с целью упрощения расчетных выкладок диаграммы деформирования реальных материалов, в том числе неупругих, сильно упрощаются. Широко применяется гипотеза о нелинейно-упругом материале, согласно которой зависимости между напряжениями и деформациями при нагрузке и разгрузке тождественны. В то время как зависимости «напряжение – деформация» могут иметь различное аналитическое представление, для неупругих материалов часто используются упрощенные диаграммы деформирования: билинейные с упрочнением, билинейные идеально упругопластические, параболические с площадкой текучести и иные.

В статье излагаются критерии соответствия конечных элементов континуальных объектов и эквивалентных шарнирно-стержневых структур, предлагаются усовершенствованные численно-аналитические методы расчета напряженно-деформированного состояния и оптимизации строительных сооружений. Рассматриваются специальные вопросы колебаний и устойчивости линейно и нелинейно (физически, геометрически, конструктивно, топологически и т. д.) деформируемых плоских и пространственных шарнирно-стержневых систем.

Метод стержневой аппроксимации в задачах расчета стержневых и континуальных систем

Рассмотрим пространственную шарнирно-стержневую систему (элементарной ячейкой которой является кубическая решетка с диагоналями граней и внутренними диагоналями), моделирующую сплошную упругую среду. Напряженное состояние упругой среды и аппроксимирующей ее стержневой системы будем считать эквивалентными, если перемещения узлов стержневой системы и соответствующих им точек сплошной среды будут одинаковыми.

Выражение для определения матрицы упругих коэффициентов шарнирно-стержневой системы получено в [2] и имеет вид:

где С – матрица преобразования компонентов деформаций:

Н – матрица площадей граней куба, приходящихся на один стержень каждого направления;

К – диагональная матрица с элементами:

Второй критерий перехода от сплошной упругой среды к шарнирно-стержневой структуре можно получить, сравнивая матрицы жесткостей конечного элемента упругой среды и шарнирно-стержневого блока. Например, для конечного элемента в форме параллелепипеда три элемента первого столбца матрицы жесткости (размером 24х24) имеют вид:

где a, b, c – длина ребра вдоль оси x, у, z соответственно;

m – коэффициент Пуассона.

Соответствующие три элемента матрицы жесткости (размером 24х24, модуль Е в последующем опущен) шарнирно-стержневого блока имеют вид:

где а – длина ребра куба;

b – длина диагонали грани;

c – длина внутренней диагонали;

EA1 – жесткость стержня, параллельного координатной оси;

EA2 – жесткость диагонального стержня, расположенного на грани;

EA3 – жесткость внутреннего диагонального стержня.

Общий подход к совместному учету переменных проектирования в задаче оптимального проектирования конструкций

Совместный учет переменных проектирования (ПП), а именно площадей поперечных сечений «В» и общей высоты конструкции «h» по методу локальных линеаризованных областей [1], возможен при рассмотрении уравнений состояния и ограничений как функций трех переменных. В этом случае для функции Н(В, h, z) = 0 возможна следующая линеаризованная запись:

Отсюда следует, что:

(1)

Функции ограничений при таком подходе также должны рассматриваться как зависимые от тех же ПП, т. е. y = y(В, h, z). Следовательно:

Используя уравнение (1), получим:

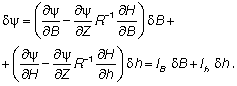(2)

Одинаковый порядок матриц I_B и I_h позволяет записать выражение (2) в виде:

(3)

Целевая функция (масса или объем материала) задачи оптимизации стержневой системы представляется следующим выражением:

где L⁽⁰⁾_k – суммарная длина стержней k-й группы ПП по «В», не зависящая от переменной h;

L_k(h) – суммарная длина стержней той же группы, зависящая от h.

Приращение функции y₀ может быть представлено в виде:

(4)

Частные производные определяются по выражениям:

где L_k – суммарная длина стержней k-й группы по «В».

Сумма берется по стержням, включаемым в одну группу ПП по «В».

Выражение (4) можно записать следующим образом:

Используя равенство порядков матриц I⁽⁰⁾_B и I⁽⁰⁾_h, представим уравнение (4) в следующей форме:

(5)

При вычислении ¶H/¶h, ¶y/¶h, ¶y₀/¶h необходимо иметь в виду, что a = a(h). Следовательно, sina = sina(h), cosa = cosa(h).

На основе полученных выражений можно решить следующую задачу ЛП:

(6)

Определение компонент вектора запасов производится по описанной в работе методике.

Изложенный подход к формированию ММ можно расширить и на случай трех ПП (третьей ПП может быть модуль упругости материала Е). Тогда выражения (3) и (5) будут записываться в виде:

(7)

(8)

Постановки задачи оптимизации системы с одной группой ПП получаются как частные из описанной. Следует отметить, что изложенный подход является общим. В качестве показателя качества проекта может приниматься любая функциональная зависимость, определяющая объем материала, стоимость конструкции и т. п.

Численная реализация задачи для ПП типов «В» и «h» выполнена по двум вариантам.

1. В соответствии с алгоритмом А1 на каждом шаге продвижения к оптимальному плану оценивается влияние каждой группы ПП на приращение показателя качества. Найденные приращения сравниваются. Большее значение приращения определяет ту группу ПП, которая изменяет параметры проекта. Программы вычислений (ОРК1, ОРК2), реализующие этот алгоритм, написаны для исследовательских задач (ОРК1) и для задач реального проектирования (ОРК2).

2. ПП «В» и «h» совместно определяют параметры нового проекта на каждом шаге оптимизации (программа ОРК3).

Исследования проведены на тестовых примерах.

Теоретические основы расчета физически, геометрически и конструктивно нелинейных шарнирно-стержневых систем

В проводимых исследованиях учитываются произвольные диаграммы деформирования конструкционных материалов, задаваемые либо аналитически, либо в табличной форме. Последнее обстоятельство дает возможность применения реальных диаграмм деформирования, снятых прямо с испытательной машины. В этом состоит одно из основных отличий проводимых исследований от известных решений, полученных другими авторами.

Закон физической нелинейности может быть как симметричным (относительно растяжения–сжатия), так и несимметричным. Разработана методика учета остаточных деформаций в материале элементов сооружения при его повторно-переменном нагружении.

При первичном нагружении деформирование элемента соответствует исходной кривой деформирования. Первичная разгрузка происходит с модулем разгрузки уже по прямой до снятия напряжений. Изменение деформаций в отрицательной области напряжений при изменении направления нагрузки происходит в соответствии с начальным законом деформирования. Цикл нового нагружения совершается по линейному закону с модулем разгрузки до достижения напряжений, зафиксированных на предыдущем этапе. Дальнейшее нагружение совершается по исходному закону деформирования.

Численным экспериментом выявлено, что даже при монотонном изменении нагрузки (при простом нагружении) изменение нелинейных деформаций упругопластических тел может быть немонотонным, знакопеременным. При достаточно большом количестве циклов повторно-переменного нагружения область упруго-пластической работы материала сужается, и достигается предельное состояние.

Нелинейный расчет шарнирно-стержневых систем ведется с учетом как больших перемещений, так и больших деформаций [3] шаговым методом дифференцирования по параметру нагружения. Конструктивная нелинейность в проводимых исследованиях рассматривается как частный случай физической нелинейности. Рассматриваются диаграммы деформирования, моделирующие люфты и натяги в элементах сооружений, их выключение из работы или разрушение. Это исключает разработку специальных алгоритмов и программных модулей для учета односторонних связей.

Устойчивость состояний равновесия нелинейных систем

Учет больших перемещений и больших деформаций является отличительной особенностью исследований, так как в других известных исследованиях по нелинейным расчетам рассматриваются большие перемещения, но малые деформации, что не позволяет в определенных ситуациях учесть в полной мере деформированную схему сооружения (разрушение элемента, сохранение усилия в элементе при его вытягивании через блок и т. п.).

Нелинейное деформирование рассматривается как процесс последовательного, шагового перехода от одного равновесного состояния к другому по мере изменения параметра нагружения. В любом установившемся состоянии равновесия параметр нагружения может быть изменен. Может быть изменена и расчетная схема деформируемого объекта (учтена топологическая нелинейность). Но каждый новый шаг деформирования (новая нагрузка или воздействие, разгрузка, изменение расчетной схемы и т. п.) происходит с учетом предшествующего напряженно-деформированного состояния, а результаты суммируются, т. е. учитывается история деформирования.

Алгоритм расчета составлен так, что каждое состояние мгновенного равновесия проверяется на устойчивость качественным динамическим (энергетическим) методом [3, 5]. Процесс деформирования может быть продолжен только при условии устойчивости предыдущего состояния мгновенного равновесия. Выполняется это автоматически при факторизации матрицы мгновенной жесткости на достигнутом этапе деформирования путем проверки ее положительной определенности. Положительная определенность матрицы мгновенной жесткости свидетельствует о возможности деформированной системы совершать малые свободные колебания около данного деформированного состояния равновесия в соответствии с частотно-амплитудным уравнением:

(9)

где R – матрица мгновенной жесткости сооружения в текущем деформированном состоянии;

w – собственная частота малых колебаний относительно этого состояния;

M – матрица масс текущего состояния равновесия;

– соответствующий собственный вектор (собственная форма).

Это дает возможность оценить динамические характеристики уже деформированного сооружения (собственные частоты и собственные формы колебаний в конкретном деформированном состоянии). Известные программные комплексы решают подобную задачу только для линейно деформируемых систем и только в недеформированном состоянии.

Дополнительно разработан критерий устойчивости мгновенных состояний равновесия нелинейно деформируемых систем, в составе которых находятся элементы с почти нулевой жесткостью (элементы в пластическом состоянии) и элементы с почти нулевой податливостью (близкие к бесконечно жестким). Анализ устойчивости таких систем сводится к исследованию знаковой определенности квадратичной формы, которая приведена в левой части преобразованного уравнения свободных колебаний:

(10)

где – вектор приращений обобщенных усилий в жестких элементах;

D – матрица податливости жестких элементов (в пределе нулевая).

Первое слагаемое этой формы (10) выражается через обобщенные перемещения узлов системы, жесткости только деформируемых элементов, включая элементы в пластическом состоянии (r_ik = 0) и текущие усилия во всех элементах системы (в том числе и жестких), а второе – через обобщенные приращения усилий только в жестких (почти недеформируемых) элементах (элементы с нулевой податливостью (d_jj = 0) автоматически исключаются из рассмотрения).

Разработан специальный алгоритм оценки устойчивости равновесия неупругих систем, основанный на поиске формы потери устойчивости с наименьшей отпорностью. На основе динамического метода решение сводится к минимизации специальной квадратичной формы, матрица мгновенной жесткости которой зависит от искомого решения:

(11)

Если наименьшая собственная частота принимает положительное значение, то исследуемое состояние равновесия устойчиво. Если же одна из собственных частот окажется мнимой или нулевой, то состояние равновесия исследуемой системы неустойчиво или является критическим.

Особенности динамических расчетов нелинейных систем

Разгрузка того или иного упругопластического элемента (растянутого или сжатого стержня) характеризуется переломом на кривой деформирования и соответственно разрывными жесткостными параметрами. Если в процессе нелинейного деформирования деформации и напряжения в некотором элементе достигли уровня (e^о, s^о), то при дальнейшем нагружении в соответствии с теорией шагового нагружения приращения деформаций и напряжений могут быть рассмотрены как конечные малые. В пределах малых приращений любую нелинейную зависимость между напряжениями и деформациями можно аппроксимировать билинейной зависимостью либо с помощью касательных, либо с помощью секущих, угловые коэффициенты которых (мгновенные модули деформирования, жесткости) различны при догрузке и разгрузке. Билинейная аппроксимация одинаково применима в пределах малых приращений как к неупругим материалам, так и к нелинейно-упругим.

Таким образом, на настоящий момент задача о малых колебаниях нелинейных систем может быть исследована достаточно полно.

В динамических задачах принимаются к рассмотрению произвольные нелинейные законы демпфирования, а не только вязкое трение. Учитываются различные динамические нагрузки и рассматриваются переходные процессы, а не только установившиеся режимы гармонических колебаний.

Разработан алгоритм прямого интегрирования дифференциальных уравнений движения геометрически и физически нелинейных шарнирно-стержневых систем, составлена и отлажена базовая компьютерная программа численного расчета рамных систем в режиме переходных процессов на произвольные динамические и статические воздействия. Уравнения движения деформируемой системы решаются без дополнительных преобразований численно одношаговыми методами до четвертого порядка точности. Численным экспериментом доказана устойчивость вычислительного процесса решения. Решена проблема учета недеформируемых связей без нарушения структуры глобальной матрицы жесткости. Данная разработка позволяет исследовать реальные процессы деформирования при динамических и статических нагрузках и воздействиях.

Созданные алгоритмы и составленные программные комплексы дают возможность учесть пространственную инерционность элементов, в том числе и таких гибких элементов как, например, оттяжки мачт, затяжки арок, элементы подвески.

Во многих известных программных комплексах инерционностью оттяжек пренебрегают. Более того, полагают, что такие конструктивные элементы как оттяжки мачт (ванты, гибкие нити, подвески) не сопротивляются кинематическим перемещениям, нормальным к хорде элемента. В проводимых исследованиях учитывается как продольная, так и поперечная жесткость (пусть, и малая) провисающих оттяжек и других растянутых элементов. А также снижение поперечной жесткости сжатых элементов. Данные исследования использованы для верификации расчетов вантового покрытия культурно-спортивного комплекса «Минск-Арена», в том числе в экстремальной ситуации (разрушение одной из несущих вант), а также при расчете ряда антенно-мачтовых и других сооружений.

заключение

1 Разработанная шарнирно-стержневая модель-аналог упругого тела позволяет проводить линейные и нелинейные расчеты напряженно-деформированных состояний континуальных систем и осуществлять их оптимизацию.

2 Создана теория, разработаны методы, алгоритмы и компьютерные программы расчета на прочность, жесткость, устойчивость и колебания стержневых нелинейно деформируемых систем.

3 Разработанные методы, алгоритмы и компьютерные программы были применены для расчета на прочность, жесткость, устойчивость и колебания ряда реальных объектов.

Список литературы

1. Борисевич, А. А. Оптимизация нелинейно-упругих стержневых систем по методу локальных линеаризованных областей / A. А. Борисевич. – Брест: Издательство БрГТУ, 2001. – 104 с.

2. Борисевич, A. А. Метод стержневой аппроксимации в задачах анализа напряженно-деформированного состояния стержневых и континуальных систем / A. А. Борисевич // Строительная наука и техника. – 2006. – № 3. – С. 75–80.

3. Сидорович, Е. М. Нелинейное деформирование, статическая и динамическая устойчивость пространственных стержневых систем / Е. М. Сидорович. – Минск: БГПА, 1999. – 200 с.

4. Сидорович, Е. М. Особенности расчета и работы нелинейно деформируемых пространственных вантовых систем / Е. М. Сидорович // Перспективы развития новых технологий в строительстве и подготовке инженерных кадров Республики Беларусь: сб. тр. XV Междунар. науч.-метод. семинара: в 2-х т.; под общ. ред. Д. Н. Лазовского, А. А. Хотько. – Новополоцк: ПГУ, 2008. – Т. 1. – С. 46–52.

5. Борисевич, А. А. Строительная механика: учебное пособие для вузов / А. А. Борисевич, Е. М. Сидорович, В. И. Игнатюк. – Издание второе, переработанное. – Минск: БНТУ, 2009. – 756 с.