В статье представлена верификация вариационно-разностного подхода, предложенного ранее одним из авторов для решения контактных задач. Верификация осуществляется путем сравнения результатов линейных и нелинейных расчетов с использованием вариационно-разностного подхода и результатов, полученных с помощью современных компьютерных комплексов Ansys, Femap (Nastran), методом расчета в которых является метод конечных элементов. Рассматривается контактная задача нелинейной теории упругости применительно к расчету нелинейно упругого неоднородного основания (со слабым слоем) под балочной плитой.

This article describes the verification of the variational-differential approach proposed by one of the authors for solving contact problems. The verification is done by comparing linear and nonlinear calculations performed by using the varational-differential approach and the results obtained with the help of computer software complexes Ansys, Femap (Nastran) based on the finite element method. A contact problem of the nonlinear theory of elasticity has been considered with reference to the calculation of a nonlinear-elastic inhomogeneous base (with a weak layer) under the beam slab.

ВВЕДЕНИЕ

Расчет нелинейно упругого неоднородного основания под балочной плитой – одна из разновидностей контактных задач нелинейной теории упругости. Для ее решения авторами используется вариационно-разностный подход (ВРП): модификация вариационного метода – в нелинейной постановке и с использованием метода конечных разностей. Предлагаемый подход позволяет полностью описать напряженно-деформированное состояние (НДС) нелинейно упругого основания, исследовать контактную зону «плита–основание», вычислить осадки основания и внутренние усилия в балочной плите. В силу нелинейности рассматриваемая задача решается методом упругих решений в форме переменных параметров упругости, через итерационный алгоритм, численная реализация которого осуществляется методом конечных разностей в программном пакете Mathematica.

Известны преимущества вариационных методов при решении задач математической физики. Зачастую именно эти методы позволяют избежать сложных и громоздких выкладок и быстро получить нужный результат с приемлемой для инженера точностью. В задачах статического и динамического расчета конструкций один из вариационных принципов (принцип Лагранжа) характеризует тот факт, что в состоянии статического равновесия любая конструкция деформируется таким образом, что ее полная потенциальная энергия обладает минимумом.

Однако на сегодняшний день в научной литературе недостаточно полно освещено применение вариационных методов в контактных задачах линейной и нелинейной теории упругости. Такое положение объясняется сложностью решения контактных задач, особенно для изгибаемых элементов конструкций.

Множество задач для балок и плит на основании Винклера рассчитал в аналитическом виде великий русский механик, профессор С. П. Тимошенко [1]. В своих расчетах он использовал прямой метод решения вариационных задач – метод Ритца. Осесимметричную задачу для круглой пластины на упругом полупространстве методом Ритца рассмотрел A. P. S. Selvadurai [2]. Позднее этот подход с некоторыми изменениями был использован в работах С. В. Босакова [3, 4] при решении различных контактных задач теории упругости и строительной механики. Ряд работ по решению контактных задач вариационными методами освещен в коллективной монографии [5].

В современных расчетах учитываются не только сложность формы тела и разнообразие воздействия (силовое, температурное и т. п.), но и специфика физических свойств материалов, из которых изготовлены тела. Учет физической, геометрической или конструктивной нелинейности контактирующих тел в связи с цикличностью итерационного алгоритма усложняет расчеты на порядок. Для упрощения расчетов, но без потери точности, в нелинейной теории упругости предпочтение отдается приближенным методам решения задач о деформировании твердых тел.

ПОСТАНОВКА КОНТАКТНОЙ ЗАДАЧИ

Основу решения контактной задачи составляет поиск закона распределения реактивных давлений на контакте конструкции с упругим основанием, которое сложным образом зависит от жесткости конструкции, упругих характеристик основания, внешней нагрузки, характера закрепления конструкции. Подробные сведения о методах решения контактных задач и моделях упругого основания можно найти в работах [5–7].

При постановке контактной задачи нелинейной теории упругости (плоская деформация) неоднородная среда моделируется как слоистое основание: рассматривается нелинейно упругое неоднородное основание под линейно упругой балочной плитой, имеющее область местных ослаблений (торфяная линза). Плита находится под действием внешней нагрузки q(x). Параметры плиты: ширина 2l, высота h, изгибная жесткость EJ.

При решении задачи используются следующие гипотезы и допущения теории упругости: в зоне контакта плиты с упругим основанием возникают только нормальные напряжения (реактивные давления), силы трения пренебрежительно малы; для балочной плиты справедливы гипотезы теории изгиба. Неоднородное основание при расчете заменяется прямоугольной расчетной областью, на границах которой u = 0, v = 0; в контактной зоне справедливо равенство осадок основания прогибам плиты.

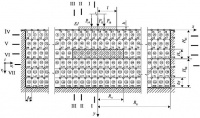
Основание аппроксимируется симметричной разбивочной сеткой конечных размеров (29x7) с постоянным шагом по осям: X -Dх, Y - Dy (рис. 1). В результате разбивки расчетной области получена расчетная модель из 203 i-х узловых точек и 168 j-х сеточных ячеек. Первые 84 ячейки (1−84) принадлежат верхнему упругому слою, вторые 84 ячейки (85−168) – нижнему. Область местных ослаблений соответствует 67−74 сеточным ячейкам. Аналогичная постановка контактной задачи, граничные условия и расчетная модель упругого основания приводятся в работах [8, 9].

Рис. 1. Расчетная модель

Узловые точки 12−18 являются контактными (см. рис. 1), то есть одновременно точками основания и плиты в контактной зоне. В точках 14, 15, 16 внешняя нагрузка на плиту q(x) заменяется системой сосредоточенных сил P₁₄ = P₁₆ = P, P₁₅ = 2P (см. рис. 1).

За неизвестные принимаются: u_i(x), ν_i(y) - компоненты вектора перемещения i-й узловой точки основания; p_y⁽ⁱ⁾(x, y) − реактивные давления (контактные напряжения) в зоне контакта плиты с основанием.

Для каждого слоя упругого основания выбирается модель упругого слоя конечной толщины с переменным модулем деформации E_k, который изменяется функционально, в неявном виде, и входит в закон нелинейно упругого деформирования основания s_i = Ф(e_i). Коэффициент Пуассона упругого слоя n_k в силу малости своего изменения принимается постоянным. Такое моделирование упругого основания предлагается и обосновывается в работе [10].

Закон нелинейно упругого деформирования основания s_i(e_i) описывается математически в виде функции «гиперболический тангенс»:

(1)

где s_yk- предел текучести;

E_0k - начальный модуль деформации k-го слоя упругого основания.

Теория нелинейных расчетов неоднородных оснований с использованием функции «гиперболический тангенс» приведена в [8, 9].

ВАРИАЦИОННО-РАЗНОСТНЫЙ ПОДХОД

Сформулированная задача решается в нелинейной постановке с использованием функционала полной энергии расчетной модели «плита − основание». Функционал полной энергии Э получается суммированием функционала энергии деформаций упругого основания U_f, функционала энергии изгиба плиты W_b и потенциала работы внешней нагрузки П:

(2)

Каждое из слагаемых в формуле (2) определяется соотношениями, приведенными в [8, 9].

Нелинейный расчет балочной плиты на нелинейно упругом неоднородном основании методом упругих решений предполагает итерационный процесс. При каждой итерации модуль деформации в i-й точке упругого слоя основания изменяется, поэтому при вычислениях используется переменный (касательный) модуль деформации, определяемый в следующем виде:

(3)

В первом приближении сформулированная задача нелинейного расчета решается в линейной постановке (нулевая итерация). По вычисленным значениям перемещений i-й узловой точки u_i(x), ν_i(y) определяются интенсивность деформаций и интенсивность напряжений в центрах сеточных ячеек.

Имея значения напряжений и перемещений, полученных в результате решения задачи в первом приближении, определяется касательный модуль деформации для каждой j-й сеточной ячейки (3), и задача решается во втором и последующих приближениях (первая и вторая итерация соответственно). Итерационный процесс заканчивается, как только разница между последующим и предыдущим приближениями исследуемой функции будет соответствовать требуемой точности решения задачи.

ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧИ МЕТОДОМ КОНЕЧНЫХ ЭЛМЕНТОВ

Современная техника и компьютерные программы позволяют использовать численные методы для решения систем дифференциальных и алгебраических уравнений большого порядка. Так, в статье В. Г. Федоровского и С. Г. Безволева [6] предлагается реализация итеративного алгоритма Шварца для расчета упругой плиты на любой модели упругого основания методом конечных элементов (МКЭ).

Существует большое количество программных комплексов, использующих МКЭ для определения напряжений, деформаций и перемещений, а также для проверки условий прочности и устойчивости в сложных геотехнических системах с учетом совместной работы инженерных конструкций. Наиболее универсальными из современных комплексов являются Nastran (Femap) и Ansys.

Для оценки корректности линейных и нелинейных решений, полученных с помощью описанного выше вариационно-разностного подхода, было выполнено моделирование и решение принятой задачи с помощью МКЭ в реализации отмеченных комплексов. Для конечно-элементного (КЭ) анализа введены те же исходные данные, что и в вариационно-разностном подходе, включая размер сетки.

В принятых КЭ моделях используются элементы плоской деформации (PLANE STRAIN) и жесткие связи (RIGID). Материал упругих слоев неоднородного основания и балочной плиты – изотропный. Связь между плитой и основанием – на жестких элементах в направлении вертикальной оси Y.

Нелинейно упругие (nonlinear elastic) свойства материалов заданы нелинейной зависимостью «s – e», аппроксимированной кусочно-линейной функцией (рис. 2).

Рис. 2. Диаграммы нелинейно-упругого деформирования (послойно)

РЕЗУЛЬТАТЫ РАСЧЕТА С ИСПОЛЬЗОВАНИЕМ ВРП И МКЭ

При числовой апробации алгоритма нелинейного расчета использовались следующие параметры инженерной системы «балочная плита - упругое основание»: 1-й слой основания (песок средней плотности) - s_y1 = 0,20 МПа, n₁ = 0,3, E₀₁ = 25 МПа; второй слой основания (суглинок) -s_y2 = 0,25 МПа, n₂ = 0,33, E₀₂ = 30 МПа; местные ослабления (торфяная линза) -s_y2 = 0,055 МПа, n₂ = 0,35, E₀₂ = 6 МПа; железобетонная плита (бетон класса С²⁵/₁₀) - E_b = 2,35×10¹⁰ Па, l = 1,2 м, h = 0,5 м.

На рис. 3 представлены эпюры осадок поверхности расчетной области основания, полученные как результаты расчетов с использованием ВРП (численная реализация МКР в программном пакете Mathematica) и МКЭ (в реализации программного комплекса Femap (Nastran)).

На рис. 4, 5 приведены результаты линейного и нелинейного расчетов с использованием МКЭ в численной реализации программного комплекса Femap (Nastran): осадки основания и распределение напряжений в пределах принятой расчетной области.

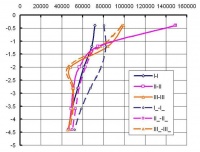
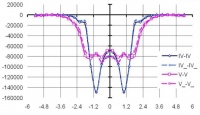
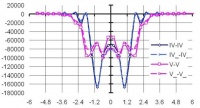
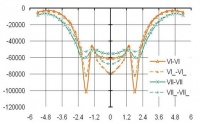
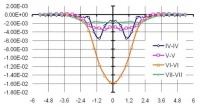
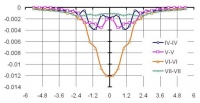
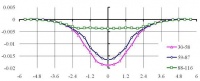
На рис. 6–8 представлены эпюры напряжений в центрах ячеек расчетной области по вертикальным и горизонтальным сечениям (см. рис. 1), позволяющие сопоставить линейные и нелинейные решения в напряжениях при использовании: МКЭ (а); ВРП (б).

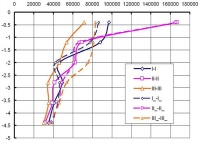
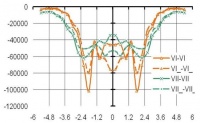
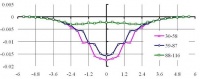
На рис. 9 представлены эпюры деформаций в центрах ячеек расчетной области по горизонтальным сечениям (см. рис. 1), позволяющие сопоставить нелинейные решения в деформациях при использовании: МКЭ (а); ВРП (б).

На рис. 10 представлены эпюры вертикальных перемещений узловых точек расчетной области по горизонтальным рядам (см. рис. 1), позволяющие сопоставить нелинейные решения в перемещениях при использовании: МКЭ (а); ВРП (б).

По вертикали отложены перемещения(м), по горизонтали – расстояние от оси плиты (м)

Рис. 3. Эпюры осадок поверхности расчетной модели основания

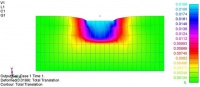
Рис. 4: а – распределение перемещений под штампом расчетной модели основания; б – напряжения по Мизесу

Рис. 5: а – максимальные касательные напряжения; б – распределение нормальных напряжений по основанию под штампом

а) б)

Основной линией показано нелинейное решение, штриховой – линейное

Рис. 6. Эпюры напряжений s_yk по глубине расчетной области для вертикальных сечений при использовании: а – МКЭ; б – ВРП

а) б)

Основной линией показано нелинейное решение, штриховой – линейное

Рис. 7. Эпюры напряжений s_yk по ширине расчетной области для горизонтальных сечений верхнего слоя при использовании: а – МКЭ; б – ВРП

а) б)

Основной линией показано нелинейное решение, штриховой – линейное

Рис. 8. Эпюры напряжений s_yk по ширине расчетной области для горизонтальных сечений нижнего слоя при использовании: а – МКЭ; б – ВРП

а) б)

Рис. 9. Эпюры деформаций (нелинейное решение) по ширине расчетной области при использовании: а – МКЭ; б – ВРП

Рис. 10. Эпюры вертикальных перемещений узловых точек расчетной модели (нелинейное решение) при использовании: а – МКЭ; б – ВРП

СРАВНЕНИЕ РЕЗУЛЬТАТОВ

Необходимость представления значительного количества графиков продиктована тем фактом, что в решении нелинейных задач учувствуют непропорциональные параметры (s, e), и для оценки корректности решений, по мнению авторов, необходимо сравнение результатов в напряжениях, деформациях и перемещениях характерных точек (центров ячеек или узловых точек) неоднородного упругого основания, для разных сечений его расчетной модели.

Для сравнения результатов нелинейных расчетов вводится показатель отклонений, рассчитываемый по формуле

(4)

где Df – относительная разница в значениях величины f, вычисленной в каждом из расчетов;

f ^(s,t)_max, f ^(s,t)_min – максимальное и минимальное значения величины f соответственно;

f_s, f_t - значение получено для слоистого основания с использованием МКЭ и ВРП.

Максимальное значение осадки поверхности расчетной модели основания, полученное с использованием МКЭ и ВРП в линейной постановке, составляет 15,03 и 13,92 мм (показатель отклонения Df = 7,3 %), в нелинейной постановке – 19,81 и 17,89 мм (показатель отклонения Df = 4,7 %).

Некоторые различия в осадках, напряжениях и деформациях могут быть объяснены следующим образом:

– в нелинейном расчете с использованием МКЭ переменный модуль деформации был представлен в виде секущего модуля, так как нелинейно упругие свойства материалов заданы нелинейной зависимостью «s – e», аппроксимированной кусочно-линейной функцией;

– в нелинейном расчете с использованием ВРП переменный модуль деформации был задан касательным.

ЗАКЛЮЧЕНИЕ

1 Авторами для линейных и нелинейных расчетов упругого основания с учетом физической нелинейности были использованы два метода:

– вариационно-разностный подход, который численно реализуется методом конечных разностей в программном пакете Mathematica;

– метод конечных элементов в реализации программных комплексов Femap (Nastran) и Ansys.

2 Сравнение результатов показало хорошее согласование параметров напряженно-деформированного состояния нелинейно упругого неоднородного основания под балочной плитой, полученных с использованием вариационно-разностного подхода и метода конечных элементов, и подтвердило корректность алгоритма нелинейного расчета с использованием метода упругих решений в итерациях и достоверность получаемых результатов. Следовательно разработанная для вариационно-разностного подхода компьютерная программа может быть использована для инженерного расчета реальных слоистых оснований по второму предельному состоянию.

СПИСОК ЛИТЕРАТУРЫ

1. Тимошенко, С. П. Устойчивость стержней, пластин и оболочек / С. П. Тимошенко. − М.: Наука, 1971. − 807 с.

2. Selvadurai, A. P. S. The interaction between a uniformly loaded circular plate and a isotropic elastic halfspace: a variational approach. J. Struct. Mech. – 1979. – V. 7(3). – Р. 231–246.

3. Босаков, С. В. Метод Ритца в примерах и задачах по строительной механике и теории упругости / С. В. Босаков. − Минск: БГПА, 2000. − 143 с.

4. Босаков, С. В. Метод Ритца в контактных задачах теории упругости / С. В. Босаков. − Брест: БрГТУ, 2006. − 108 с.

5. Развитие теории контактных задач в СССР; под ред. Л. А. Галина. − М.: Наука, 1976. − 493 с.

6. Федоровский, В. Г. Прогноз осадок фундаментов мелкого заложения и выбор модели основания для расчета плит / В. Г. Федоровский, С. Г. Безволев // Основания, фундаменты и механика грунтов. − 2000. − № 4. − С. 10–18.

7. Босаков, С. В. Статические расчеты плит на упругом основании / С. В. Босаков. − Минск: БНТУ, 2002. − 127 с.

8. Козунова, О. В. Нелинейный расчет балочных плит на слоистых основаниях с биогенными включениями. Геотехника Беларуси: теория и практика / О. В. Козунова. - Минск: БНТУ, 2008. − С. 37-65.

9. Босаков, С. В. Вариационно-разностный подход в решении контактной задачи для нелинейно упругого неоднородного основания. Плоская деформация. Теория расчета. Часть 1 / С. В. Босаков, О. В.Козунова // Вестник БНТУ. − 2009. − № 1. − С. 5−13.

10. Лукаш, П. А.  Основы нелинейной строительной механики / П. А. Лукаш. − М.: Стройиздат, 1978. − 204 с.